Laminar, Turbulent, and Transitional Flow: Key Differences
Advertisement
This article explores the distinctions between laminar flow, turbulent flow, and transitional flow, highlighting their key characteristics and how they relate to the Reynolds number. When it comes to fluid motion in pipes, we generally observe these three types of flow:
- Laminar Flow
- Turbulent Flow
- Transitional Flow
Let’s delve into each one.
Laminar Flow
In laminar flow, the fluid moves in smooth, parallel layers, also known as streamlines. These layers don’t mix as they travel along the flow’s direction. Imagine a calm river flowing steadily – that’s a good visual for laminar flow.
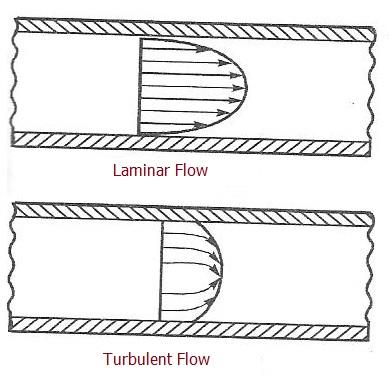
Turbulent Flow
Turbulent flow, on the other hand, is characterized by chaotic and random fluid movement. Instead of neat layers, the fluid swirls and eddies, with the average motion going parallel to the pipe axis. This type of flow is more like a rapidly flowing, choppy river. The image above visually contrasts laminar flow with turbulent flow.
Transitional Flow
Transitional flow represents a middle ground. In this case, you might find regions of both laminar and turbulent flow within the pipeline. The flow might even switch between these states intermittently. It’s not as neatly defined as the other two.
Reynolds Number: A Key Indicator
The Reynolds number (Re) is a crucial dimensionless quantity that helps us predict the type of flow. It’s essentially a ratio of inertia forces to viscous forces in the fluid.

The Reynolds number is calculated based on fluid properties. It does not account for factors like pipe roughness, bends, or valves. The equation is shown in the image above.
Here’s how the Reynolds number determines the type of flow:
- Re < 2000: The flow is laminar. Viscous forces dominate in this regime.
- Re > 4000: The flow is turbulent. Inertia forces become more significant.
- 2000 < Re < 4000: The flow is transitional. Either laminar or turbulent conditions can exist.
In summary, understanding these three types of flow, and how the Reynolds number influences them, is fundamental in fluid dynamics and various engineering applications.
Advertisement
 T&M
T&M